Applications of Linear Algebra in Portfolio Management
Published:
Linear algebra is a branch of mathematics developed to solve a system of linear equations and has found many applications in applied sciences- computer science(machine learning, image processing) and mathematical finance(portfolio management). In this article, we shall compute standard deviation of a portfolio using tools from linear algebra. Before we jump to this computation it is good to recall certain basic concepts from linear algebra.
Linear Algebra Basics
Linear Algebra is a systematic theory regarding the solutions of systems of $m$ linear equations in $n$ unknowns $x_1,x_2, \dots, x_n$ of the form
\[\begin{aligned} a_{11} x_1+a_{12} x_2+\cdots+a_{1 n} x_n & =b_1 \\ a_{21} x_1+a_{22} x_2+\cdots+a_{2 n} x_n & =b_2 \\ \vdots \quad \qquad & \quad \vdots \\ a_{m 1} x_1+a_{m 2} x_2+\cdots+a_{m n} x_n & =b_m \end{aligned}\]where the $a_{ij}$ are the coefficients (usually real or complex numbers) in front of the unknowns $x_j$, and the $b_i$ are also fixed real or complex numbers. Linear Algebra is a theory that concerns the solutions and the structure of solutions for linear equations. To get a hint of how linear algebra helps in solving some applied problems, let’s look into following puzzle.
Puzzle
Imagine yourself traveling in a river cruise ship. You noticed that the ship sailed 40 miles downstream for 4 hours and then took 5 hours sailing upstream to return to the dock. How would you calculate the speed of the ship in still water and the speed of the river current?
Solution
Let us denote speed ship in still water by $x$ and that of river current by $y$. Your observation can be now described by following system of linear equations:
\[\begin{aligned} 4(x+y) &= 40,\\ 5(x-y) &= 40. \end{aligned} \label{s1}\]The above system can be represented by the following matrix equation:
\[\begin{bmatrix} 4 & 4\\ 5 & -5 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 40\\ 40 \end{bmatrix}. \label{s2}\]By inverting the above $2\times2$ matrix we obtain the speeds as
\[\begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 9\\ 1 \end{bmatrix}. \label{s3}\]The above puzzle gives a glimpse of how one can write off a system of linear equations as one single matrix equation. If there are $n$ equations in $m$ unknowns, the order of the matrix representing the system is $n \times m$. Depending on the properties of this matrix, we may have none, unique or infinite number of solutions. In calculating the standard deviation of a portfolio we will only have to deal with case $n=m.$
Invertibility of a matrix: Let $A$ be a $n \times n$ matrix. Matrix $B$ is said to be the inverse of $A$ if $AB = BA = I$ where $I$ is the $n \times n$ identity matrix (matrix with all the diagonal entries equal to $1$ and the rest equal to $0$).
Symmetric matrix: A $n \times n$ matrix \(A = (a_{ij})_{i,j=1}^n\) is said to be symmetric if the matrix components are such that $a_{ij} = a_{ji}.$
We shall see in a short while that the variance-covariance matrix involved in computation of variance of the portfolio is a symmetric matrix.
Standard Deviation of a Portfolio
Standard deviation or volatility is a statistical measure of the dispersion of returns of a security. Volatility represents how large an asset’s prices swing around the mean price. In what follows below we demonstrate the role of linear algebra in calculating standard deviation of a portfolio.
For the sake of demonstration, let us suppose that our portfolio consists of two securities $A_1$ and $A_2$ whose returns, standard deviation and weights in the portfolio are summarized in the following table.
| Asset | Weight | Standard Deviation($\%$) | Return($\%$) |
|---|---|---|---|
| Asset1 | $x_1$ | $\sigma_1$ | $r_1$ |
| Asset2 | $x_2$ | $\sigma_2$ | $r_2$ |
The portfolio return ($r$) is the weighted average of the individual asset returns. It is given by \begin{equation} r = x_1r_1 + x_2r_2, \quad \text{ for } x_1 + x_2 =1. \end{equation}
On the other hand, the standard deviation or the volatility ($\sigma$) of the portfolio is given by \begin{equation}\label{formula} \sigma = \left(x_1^2 \sigma_1^2 + x_2^2 \sigma_2^2 + 2\rho_{12}(x_1 \sigma_1)(x_2 \sigma_2)\right)^{\frac{1}{2}} \end{equation} where $\rho_{12} \in [-1,1]$ is the correlation between assets $A_1$ and $A_2$.
At this juncture we make an important observation that is essential in developing general case of $n$ assets in the portfolio. We note that $\sigma^2$ is expressed as a quadratic form given by
\[\sigma^2 = \begin{pmatrix} x_{1} & x_{2} \end{pmatrix} \begin{pmatrix} \sigma_{1}^2 & \sigma_{1}\sigma_{2}\rho_{12} \\ \sigma_{1}\sigma_{2}\rho_{12} & \sigma_{2}^2 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} \label{QF}\]On the right hand side of the above expression, sandwiched between the weights vectors is the variance-covariance matrix. As far as the general computation is concerned, the expression \eqref{QF} is more helpful than \eqref{formula} which we will see in a short while.
Example: Let $\sigma_{1} = 23\%, \sigma_{2} = 30\%$, $r_1 = 18\%, r_2 = 25\%$, $x_1 = 0.3, x_2 = 0.7$, and $\rho_{12} = -0.08$. The the portfolio returns and standard deviation are $r = 22.9\%$ and $\sigma = 21.5737\%,$ respectively.
Suppose as a risk averse investor, one is interested in a minimum variance portfolio then what should be the weights for the assets in the portfolio? This can be calculated as below:
Firstly note that $x_2 = 1-x_1$ and the variance is
\[\sigma^2 = x_1^2 \sigma_1^2 + (1-x_1)^2 \sigma_2^2 + 2 x_1 (1-x_1) \rho_{12} \sigma_1 \sigma_2 .\]To find the weights that minimize the variance, we find the stationary points of $\sigma^2$ with respect to $x_1.$ That is we find $x_1$ such that
\[\frac{d \sigma^2}{dx_1} = 0.\]This gives
\[x_1 = \frac{\sigma_2^2 - \rho_{12} \sigma_1\sigma_2}{\sigma_1^2 + \sigma_2^2 - 2 \rho_{12}\sigma_1\sigma_2} \label{min}\]To check whether the above value for $x_1$ gives minimum variance, we compute the second derivative
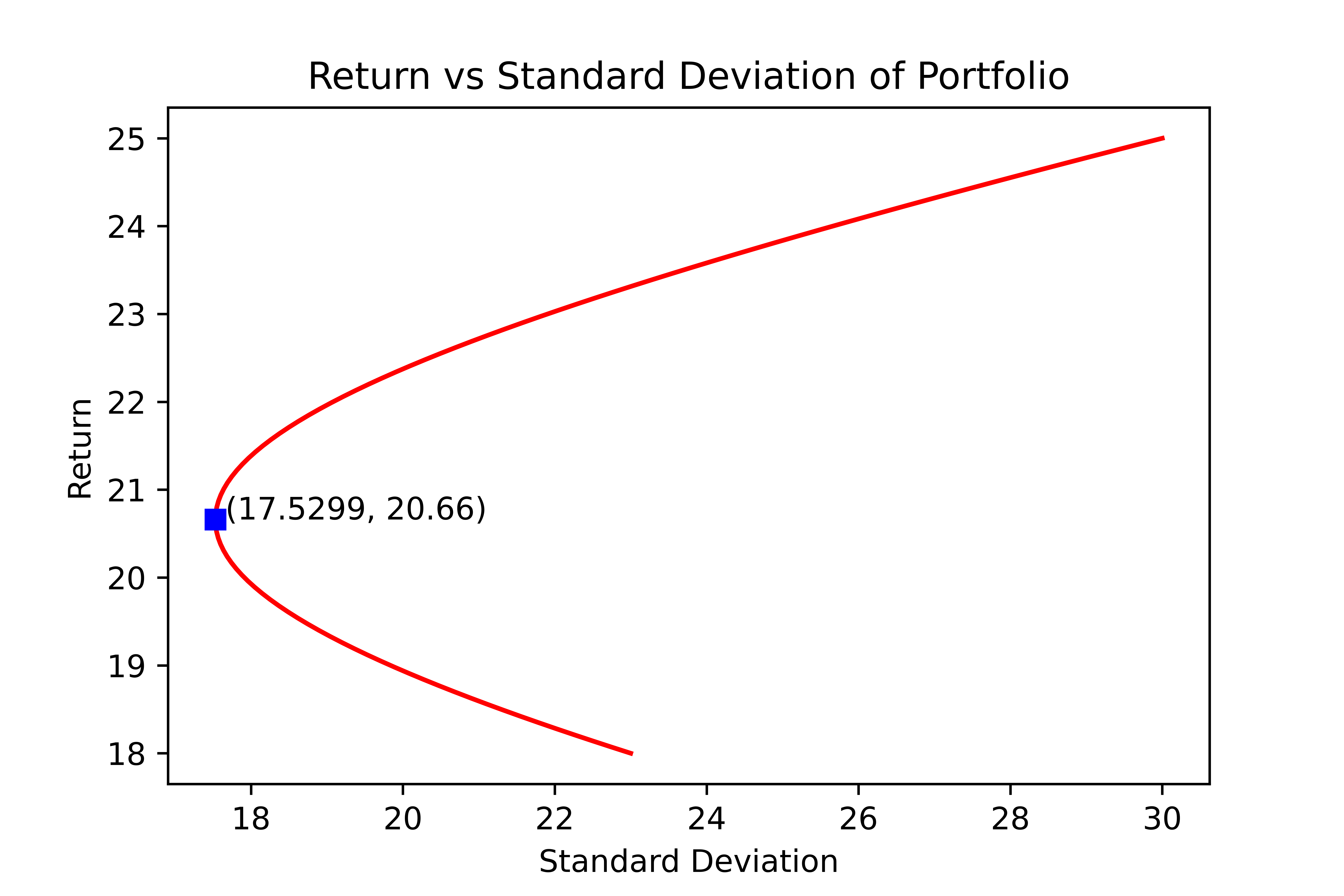
\[\frac{d^2 \sigma^2}{dx_1^2} = 2(\sigma_1^2 + \sigma_2^2 - 2 \rho_{12}\sigma_1\sigma_2) > 0 \quad \text{ for any } \rho_{12} \in [-1,1].\]Hence $x_1$ defined in \eqref{min} is the point of minimum for $\sigma^2$. For the above example, minimum variance portfolio is attained when $x_1 = 0.62$ and $x_2 = 0.38$ with $\sigma = 17.5299\%$ and $r = 20.66\%.$ The following figure shows returns vs standard deviation plot of the portfolio for various combinations of $x_1$ and $x_2.$ Python code to generate the graph can be found here.
When we have $n$ assets ($A_1, A_2, \dots, A_n$) in the portfolio, the portfolio variance, $\sigma^2$ is given by the quadratic form \begin{equation}\label{formula2} \sigma^2 = \sum_{i=1}^{n}x_i^2\sigma_i^2 + 2 \sum_{i=1}^{n} \sum_{\substack{j=1, \ j\neq i}}^{n} \rho_{ij} (x_i \sigma_i) (x_j\sigma_j) \end{equation} Now, what is the symmetric positive definite matrix defining this quadratic form? The answer is variance-covariance matrix. To elaborate on this, consider the matrix S defined by
\[S = \begin{pmatrix} \sigma_{1} & & \\ & \ddots & \\ & & \sigma_{n} \end{pmatrix}\]where $\sigma_i$ is the standard deviation of an asset $A_i$. Note that $S$ is diagonal matrix with $S_{ii} = \sigma_i$ and $S_{ij} = 0$ for $i\neq j$. The matrix $S$ contains standard deviations of each asset as its diagonal entries.
Next, consider the correlation matrix $C$ defined by
\[C = \begin{pmatrix} 1 & \rho_{12} & \dots & \rho_{1n} \\ \rho_{21} & 1 & \dots & \rho_{2n} \\ \vdots & \ddots & \dots & \vdots \\ \rho_{n1} & \dots & \rho_{nn-1} & 1 \end{pmatrix}.\]where $\rho_{ij} \in [-1,1] $ is correlation between the assets $A_i$ and $A_j$. It is worth to notice that $C$ is a symmetric matrix since $\rho_{ij} = \rho_{ji}$.
The variance-covariance matrix ($V$) is then given by
\[V = S \times C \times S.\]Subsequently, the portfolio variance is expressed as
\[\sigma^2 = \begin{pmatrix} x_{1} & x_{2} & \dots & x_n \end{pmatrix} V \begin{pmatrix} x_{1} \\ x_{2}\\ \vdots\\ x_n \end{pmatrix}\]where $x_i$ is the weight of the asset $A_i$ in the portfolio and $\sum_{i=1}^n x_i = 1.$
